Tích vô hướng của hai vectơ là một khái niệm quan trọng trong toán học, đặc biệt là trong hình học và đại số tuyến tính. Nó không chỉ giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các vectơ mà còn có nhiều ứng dụng thực tiễn trong các lĩnh vực như vật lý, kỹ thuật và khoa học máy tính. Trong bài viết này, chúng ta sẽ cùng tìm hiểu về khái niệm, tính chất và ứng dụng của tích vô hướng của hai vectơ, cùng với các ví dụ minh họa và bài tập thực hành. Hãy cùng Thư Viện Ôn Thi khám phá chủ đề này nhé!

1. Khái Niệm Tích Vô Hướng Của Hai Vectơ
1.1. Định Nghĩa
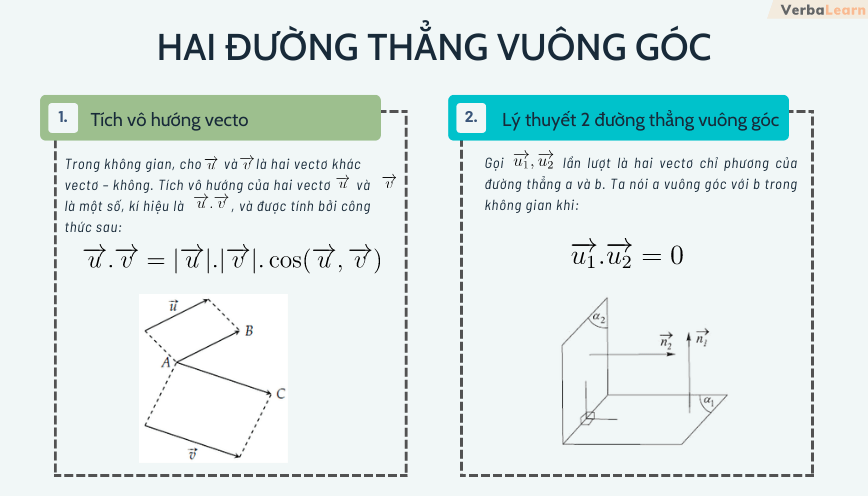
Tích vô hướng của hai vectơ (\vec{a}) và (\vec{b}) là một số thực được xác định bởi công thức:
[ \vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos \theta ]
trong đó:
- (|\vec{a}|) và (|\vec{b}|) là độ dài của các vectơ (\vec{a}) và (\vec{b}).
- (\theta) là góc giữa hai vectơ (\vec{a}) và (\vec{b}).
1.2. Biểu Thức Tọa Độ
Nếu (\vec{a} = (a_1, a_2, a_3)) và (\vec{b} = (b_1, b_2, b_3)) là hai vectơ trong không gian ba chiều, thì tích vô hướng của chúng được tính bằng:
[ \vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2 + a_3 b_3 ]
Trong mặt phẳng hai chiều, nếu (\vec{a} = (a_1, a_2)) và (\vec{b} = (b_1, b_2)), thì tích vô hướng của chúng là:
[ \vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2 ]
2. Tính Chất Của Tích Vô Hướng
2.1. Tính Chất Cơ Bản
Tích vô hướng của hai vectơ có các tính chất cơ bản sau:
- Giao hoán: (\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a})
- Phân phối: (\vec{a} \cdot (\vec{b} + \vec{c}) = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c})
- Tính chất với số vô hướng: (k(\vec{a} \cdot \vec{b}) = (k\vec{a}) \cdot \vec{b} = \vec{a} \cdot (k\vec{b}))
- Tích vô hướng của vectơ với chính nó: (\vec{a} \cdot \vec{a} = |\vec{a}|^2)
2.2. Điều Kiện Vuông Góc
Hai vectơ (\vec{a}) và (\vec{b}) vuông góc với nhau khi và chỉ khi tích vô hướng của chúng bằng 0:
[ \vec{a} \cdot \vec{b} = 0 ]
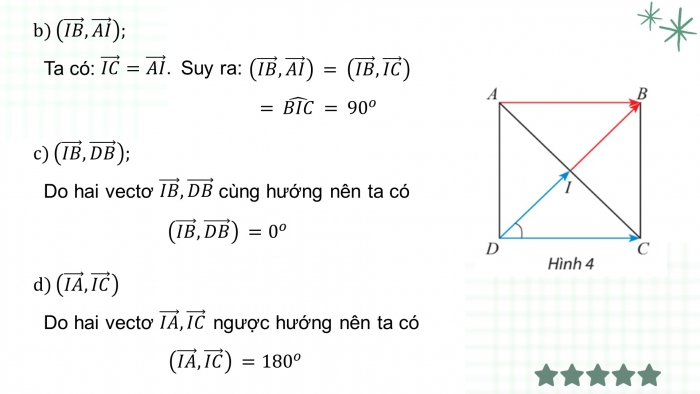
2.3. Ứng Dụng Trong Tính Góc
Từ công thức định nghĩa tích vô hướng, ta có thể suy ra công thức tính góc giữa hai vectơ:
[ \cos \theta = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|} ]
3. Ứng Dụng Của Tích Vô Hướng
3.1. Trong Hình Học
Tích vô hướng được sử dụng để tính góc giữa hai vectơ, kiểm tra tính vuông góc và tính độ dài của vectơ. Ví dụ, trong hình học không gian, tích vô hướng giúp xác định góc giữa các đường thẳng và mặt phẳng.
3.2. Trong Vật Lý
Trong vật lý, tích vô hướng được sử dụng để tính công của lực. Nếu một lực (\vec{F}) tác dụng lên một vật và làm vật di chuyển theo hướng của vectơ dịch chuyển (\vec{s}), thì công (W) được tính bằng:
[ W = \vec{F} \cdot \vec{s} ]
3.3. Trong Kỹ Thuật và Khoa Học Máy Tính
Tích vô hướng được sử dụng trong các thuật toán đồ họa máy tính để tính góc giữa các vectơ, kiểm tra tính vuông góc và tính độ dài của vectơ. Nó cũng được sử dụng trong các thuật toán học máy để tính độ tương đồng giữa các vectơ đặc trưng.
4. Ví Dụ Minh Họa
4.1. Ví Dụ 1: Tính Tích Vô Hướng Trong Mặt Phẳng
Cho hai vectơ (\vec{a} = (3, 4)) và (\vec{b} = (1, 2)). Tính tích vô hướng của chúng.
Giải:
[ \vec{a} \cdot \vec{b} = 3 \cdot 1 + 4 \cdot 2 = 3 + 8 = 11 ]
4.2. Ví Dụ 2: Tính Góc Giữa Hai Vectơ
Cho hai vectơ (\vec{a} = (1, 0, 0)) và (\vec{b} = (0, 1, 0)). Tính góc giữa chúng.
Giải:
[ \vec{a} \cdot \vec{b} = 1 \cdot 0 + 0 \cdot 1 + 0 \cdot 0 = 0 ]
[ |\vec{a}| = \sqrt{1^2 + 0^2 + 0^2} = 1 ]
[ |\vec{b}| = \sqrt{0^2 + 1^2 + 0^2} = 1 ]
[ \cos \theta = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|} = \frac{0}{1 \cdot 1} = 0 ]
[ \theta = 90^\circ ]
4.3. Ví Dụ 3: Tính Công Của Lực
Một lực (\vec{F} = (5, 0, 0)) tác dụng lên một vật và làm vật di chuyển theo hướng của vectơ dịch chuyển (\vec{s} = (2, 3, 0)). Tính công của lực.
Giải:
[ W = \vec{F} \cdot \vec{s} = 5 \cdot 2 + 0 \cdot 3 + 0 \cdot 0 = 10 ]
5. Bài Tập Thực Hành
5.1. Bài Tập 1
Cho hai vectơ (\vec{a} = (2, -1, 3)) và (\vec{b} = (4, 0, -2)). Tính tích vô hướng của chúng.
5.2. Bài Tập 2
Cho hai vectơ (\vec{a} = (1, 2, 3)) và (\vec{b} = (4, 5, 6)). Tính góc giữa chúng.
5.3. Bài Tập 3
Một lực (\vec{F} = (3, 4, 0)) tác dụng lên một vật và làm vật di chuyển theo hướng của vectơ dịch chuyển (\vec{s} = (1, 2, 2)). Tính công của lực.
6. Thư Viện Ôn Thi: Nguồn Tài Liệu Hữu Ích
6.1. Giới Thiệu Về Thư Viện Ôn Thi
Thư Viện Ôn Thi là một nền tảng trực tuyến cung cấp tài liệu học tập và ôn thi cho học sinh và sinh viên. Với hàng ngàn tài liệu phong phú và đa dạng, Thư Viện Ôn Thi giúp học sinh nắm vững kiến thức và chuẩn bị tốt cho các kỳ thi.
6.2. Tài Liệu Về Tích Vô Hướng Của Hai Vectơ (tiếp theo)
Tại thuvienonthi.com, bạn có thể tìm thấy nhiều tài liệu hướng dẫn chi tiết về tích vô hướng của hai vectơ, từ cơ bản đến nâng cao. Các tài liệu này bao gồm lý thuyết, ví dụ minh họa, và bài tập thực hành, giúp bạn nắm vững kiến thức và rèn luyện kỹ năng giải toán.
6.3. Hỗ Trợ Học Tập
Thư Viện Ôn Thi không chỉ cung cấp tài liệu mà còn có các bài giảng video, bài kiểm tra trực tuyến và diễn đàn thảo luận, giúp học sinh học tập hiệu quả và giải đáp mọi thắc mắc. Bạn có thể tham gia các khóa học trực tuyến để được hướng dẫn chi tiết và có cơ hội trao đổi với các giáo viên và bạn học khác.
7. Kết Luận
Tích vô hướng của hai vectơ là một khái niệm quan trọng trong toán học, giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các vectơ và có nhiều ứng dụng thực tiễn trong các lĩnh vực như hình học, vật lý, kỹ thuật và khoa học máy tính. Việc nắm vững khái niệm và tính chất của tích vô hướng không chỉ giúp học sinh giải quyết các bài toán phức tạp mà còn phát triển tư duy logic và khả năng phân tích.
Với sự hỗ trợ từ Thư Viện Ôn Thi, việc học tập và ôn thi trở nên dễ dàng và hiệu quả hơn bao giờ hết. Hãy truy cập thuvienonthi.com để khám phá thêm nhiều tài liệu hữu ích và nâng cao kỹ năng toán học của bạn. Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại liên hệ với Thư Viện Ôn Thi để được hỗ trợ!
Hy vọng bài viết này sẽ giúp bạn hiểu rõ hơn về tích vô hướng của hai vectơ và cách áp dụng kiến thức này vào thực tiễn. Chúc bạn học tập tốt và đạt được nhiều thành công trong các kỳ thi!
